Excelで滴定曲線を書いてみよう2
2価の酸にNaOHを加えたときの滴定曲線を電離定数から考えてみよう。
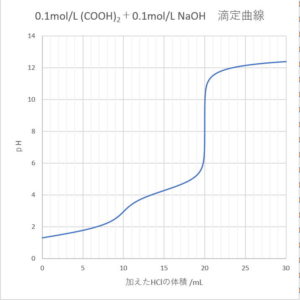
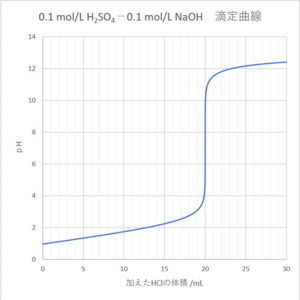
上記グラフは,硫酸の電離定数をpKa1=-5,pKa2=1.99として計算したもの。
硫酸+NaOHl滴定曲線計算値 のエクセルファイル
\(a\) mol/L H2A \(v_0\) mLに\(b\) mol/L NaOH \(v\) mLを加えたときの滴定曲線
反応後の溶液の体積:\( v_{0}+v \) mLとする
反応前のH2Aの物質量は\( av_{0} \) mmol
\( Ca=\displaystyle\frac{av_{0} \sf{ mmol}}{(v_{0}+v)\sf{ mL}} \)=\(\displaystyle\frac{av_{0}}{v_{0}+v} \) mol/L
反応前のNaOHの物質量は\( bv \) mmol
\( Cb=\displaystyle\frac{bv\sf{ mmol}}{(v_{0}+v)\sf{ mL}} \) =\(\displaystyle\frac{bv}{v_{0}+v} \) mol/Lとする。
活量1,塩の電離度を1とすると
反応後のNa+の総量:\( bv \) mmol
[Na+]=\( Cb \) 式①
\( K_1 =\displaystyle\frac{\sf{[H^+][HA^-]}}{\sf{[H_2A]}} \)
\( K_2 =\displaystyle\frac{\sf{[H^+][A^{2-}]}}{\sf{[HA^-]}} \)
\( K_1×K_2 =\displaystyle\frac{\sf{[H^+]^2[A^{2-}]}}{\sf{[H_2A]}} \)
\(\sf{[H_2A]}\)=\(\displaystyle\frac{\sf{[H^+]^2[A^{2-}]}}{K_1K_2}\)
\(\sf{[HA^-]}\)=\(\displaystyle\frac{\sf{[H^+][A^{2-}]}}{K_2}\)
式の簡略化のため \(a_1=\displaystyle\frac{ \sf{[H^+]^2} }{K_1K_2} \) \(a_2=\displaystyle\frac{ \sf{[H^+]} }{K_2} \) とする。
\(\sf{[H_2A]} \) = \(a_1\sf{[A^{2-}]}\) 式②
\(\sf{[HA^-]} \) = \(a_2\sf{[A^{2-}]}\) 式③
溶液中に存在するAが関係する物質は,H2Aから生じたものだから,
\(Ca\)とは,つぎの関係がある。
\(Ca\) =\(\sf{ [H_2A] + [HA^-] + [A^{2-}]}\)
= \(a_1\sf{[A^{2-}]}\) + \(a_2\sf{[A^{2-}]}\) + \(\sf{[A^{2-}]}\)
= \( (a_1+a_2+1) \sf{[A^{2-}]}\)
\(Z =\displaystyle\frac{1}{a_1+a_2+1} \) とする。
\(Ca =\displaystyle\frac{\sf{[A^{2-}]}}{Z} \)
\(\sf{[A^{2-}]}\) =\( ZCa\) 式④
式③,④より
\(\sf{[A^-]}\) =\( a_2ZCa\) 式⑤
電気的中性条件より,陽イオンと陰イオンの濃度には,次のような関係がある
\(\sf{[Na^+]+[H^+]=[OH^-]+[HA^-] + 2[A^{2-}]}\) 式⑥
水のイオン積 \(Kw\)=\(\sf{[H^+][OH^-]}\)より
\(\sf{[OH^-]}\)= \(\displaystyle\frac{Kw}{\sf{[H^+]}}\) 式⑦
式⑥に①,④,⑤,⑦を代入する。
\(Cb\)+\(\sf{[H^+]}\) = \(\displaystyle\frac{Kw}{\sf{[H^+]}}\) +\(a_2ZCa + 2ZCa\)
\(W = a_2Z + 2Z\) とする。
\(Cb\) +\(\sf{[H^+]}\) = \(\displaystyle\frac{Kw}{\sf{[H^+]}}\)+\( WCa\)
\(v\) が関係しているものを左辺に整理する。
\(Cb - WCa\) = \(\displaystyle\frac{Kw}{\sf{[H^+]}}\) -\(\sf{[H^+]}\)
β= \(\displaystyle\frac{Kw}{\sf{[H^+]}}\) -\(\sf{[H^+]}\) とする。
\(Cb - WCa\) =β
\(\displaystyle\frac{bv}{v_0+v}\) - \(\displaystyle\frac{Wav_0}{v_0+v}\) = β
\(v =\displaystyle\frac{βv_0+Wav_0}{b-β}\)
エクセルで,pH1~13の範囲で,\(\sf[H^+]\),\(a_1,a_2,Z,W,β\)を計算し,\(v\)を求める。